Extract cyclic results

This example uses a modal analysis with cyclic symmetry to show how to expand the mesh and results.

Note

This example requires DPF 3.0 (2022 R1) or above. For more information, see PyDPF library compatibilities.

Perform required imports

Perform required imports. This example uses a supplied file that you can get by importing the DPF examples package.

from ansys.dpf import post
from ansys.dpf.post import examples

Get Simulation object

Get the Simulation object that allows access to the result. The Simulation object must be instantiated with the path for the result file. For example, "C:/Users/user/my_result.rst" on Windows or "/home/user/my_result.rst" on Linux.

example_path = examples.find_simple_cyclic()
simulation = post.ModalMechanicalSimulation(example_path)

# print the simulation to get an overview of what's available
print(simulation)

Modal Mechanical Simulation.


Data Sources
------------------------------
/opt/hostedtoolcache/Python/3.10.19/x64/lib/python3.10/site-packages/ansys/dpf/core/examples/result_files/file_cyclic.rst

DPF Model
------------------------------
Modal analysis
Unit system: MKS: m, kg, N, s, V, A, degC
Physics Type: Mechanical
Available results:
     -  node_orientations: Nodal Node Euler Angles
     -  displacement: Nodal Displacement
     -  stress: ElementalNodal Stress
     -  elemental_volume: Elemental Volume
     -  stiffness_matrix_energy: Elemental Energy-stiffness matrix
     -  artificial_hourglass_energy: Elemental Hourglass Energy
     -  kinetic_energy: Elemental Kinetic Energy
     -  co_energy: Elemental co-energy
     -  incremental_energy: Elemental incremental energy
     -  thermal_dissipation_energy: Elemental thermal dissipation energy
     -  element_orientations: ElementalNodal Element Euler Angles
     -  structural_temperature: ElementalNodal Structural temperature
------------------------------
DPF  Meshed Region:
  51 nodes
  4 elements
  Unit: m
  With solid (3D) elements
------------------------------
DPF  Time/Freq Support:
  Number of sets: 30
Cumulative     Frequency (Hz) LoadStep       Substep        Harmonic index
1              670386.325235  1              1              0.000000
2              872361.424038  1              2              0.000000
3              1142526.525324 1              3              0.000000
4              1252446.741551 1              4              0.000000
5              1257379.552140 1              5              0.000000
6              1347919.358013 1              6              0.000000
7              679667.393214  2              1              1.000000
8              679667.393214  2              2              -1.000000
9              899321.218481  2              3              -1.000000
10             899321.218481  2              4              1.000000
11             1128387.049511 2              5              1.000000
12             1128387.049511 2              6              -1.000000
13             708505.071361  3              1              -2.000000
14             708505.071361  3              2              2.000000
15             966346.820117  3              3              2.000000
16             966346.820117  3              4              -2.000000
17             1031249.070606 3              5              -2.000000
18             1031249.070606 3              6              2.000000
19             757366.624982  4              1              -3.000000
20             757366.624982  4              2              3.000000
21             926631.623058  4              3              -3.000000
22             926631.623058  4              4              3.000000
23             1035144.649248 4              5              3.000000
24             1035144.649248 4              6              -3.000000
25             807882.379030  5              1              4.000000
26             856868.410638  5              2              4.000000
27             1063247.283632 5              3              4.000000
28             1185511.741334 5              4              4.000000
29             1278969.844256 5              5              4.000000
30             1355579.879820 5              6              4.000000

Extract expanded displacement normal

displacement_norm = simulation.displacement(
    norm=True,
    expand_cyclic=True,
)
print(displacement_norm)
displacement_norm.plot()

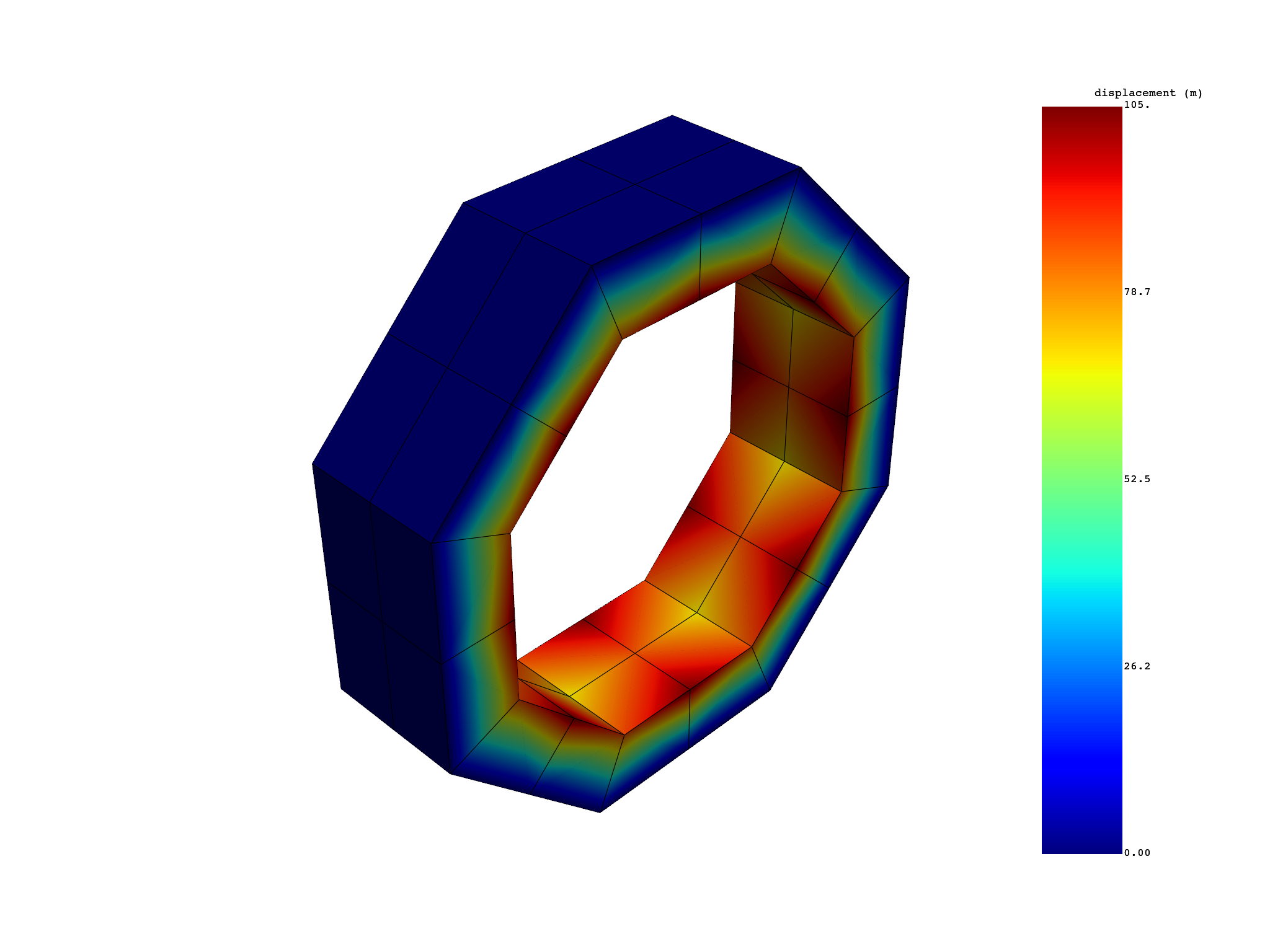
  results    U_N (m)
  set_ids          1
 node_ids
        1 8.5207e+01
       52 8.5207e+01
      103 8.5207e+01
      154 8.5207e+01
      205 8.5207e+01
      256 8.5207e+01
      ...        ...


(None, <pyvista.plotting.plotter.Plotter object at 0x7fa4ae595090>)

Extract equivalent von Mises nodal stress expanded on first four sectors

stress_vm_sectors_1_2_3_4 = simulation.stress_eqv_von_mises_nodal(
    expand_cyclic=[1, 2, 3, 4],
)
print(stress_vm_sectors_1_2_3_4)
stress_vm_sectors_1_2_3_4.plot()

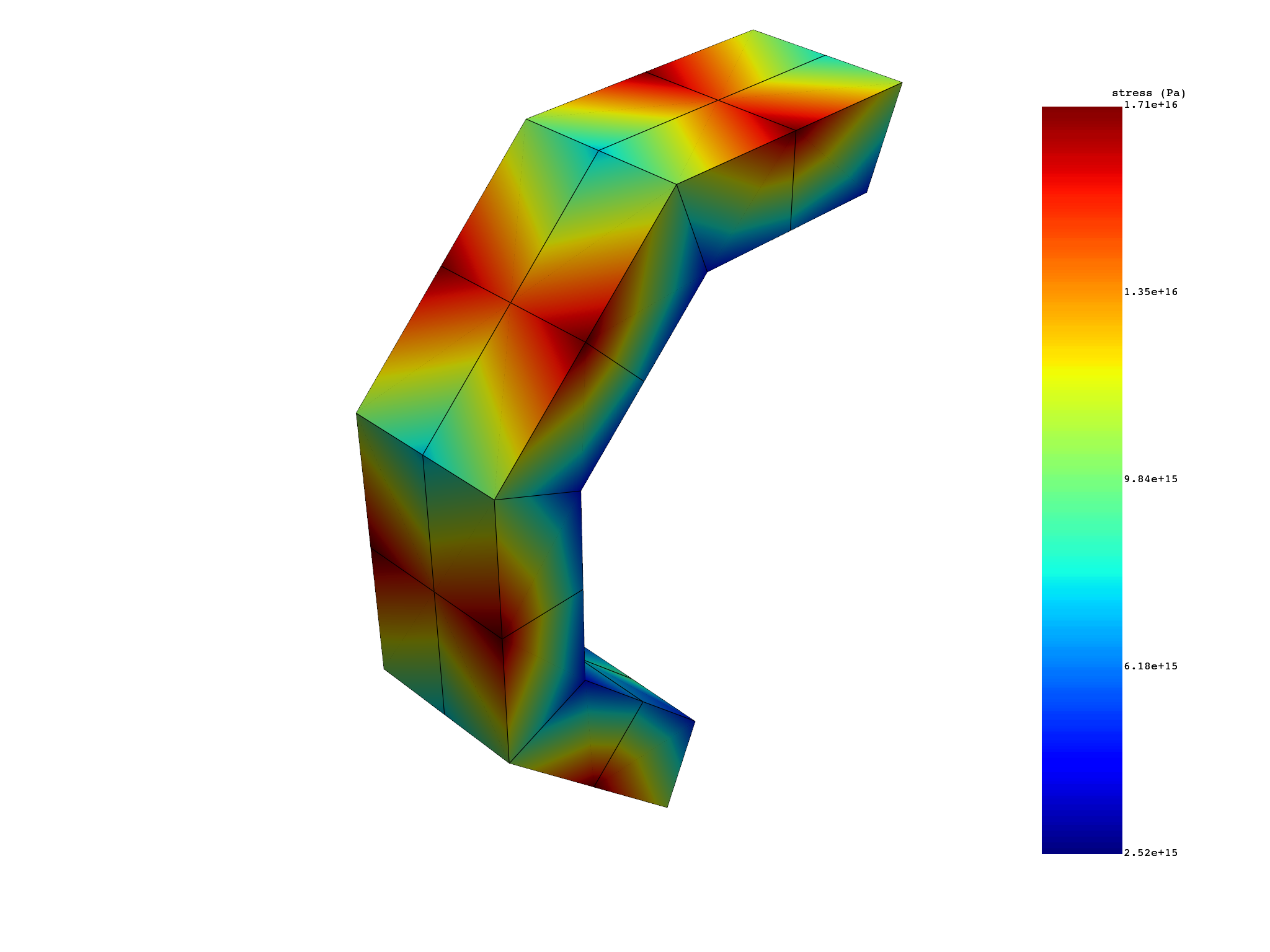
  results  S_VM (Pa)
  set_ids          1
 node_ids
        1 7.6536e+15
       14 9.2247e+15
       15 4.6219e+15
       18 6.4123e+15
        2 1.4681e+16
        6 7.9359e+15
      ...        ...


(None, <pyvista.plotting.plotter.Plotter object at 0x7fa4ae597e20>)

Extract equivalent von Mises nodal stress without expansion

stress_vm_sector_1 = simulation.stress_eqv_von_mises_nodal(
    expand_cyclic=False,
)
print(stress_vm_sector_1)
stress_vm_sector_1.plot()

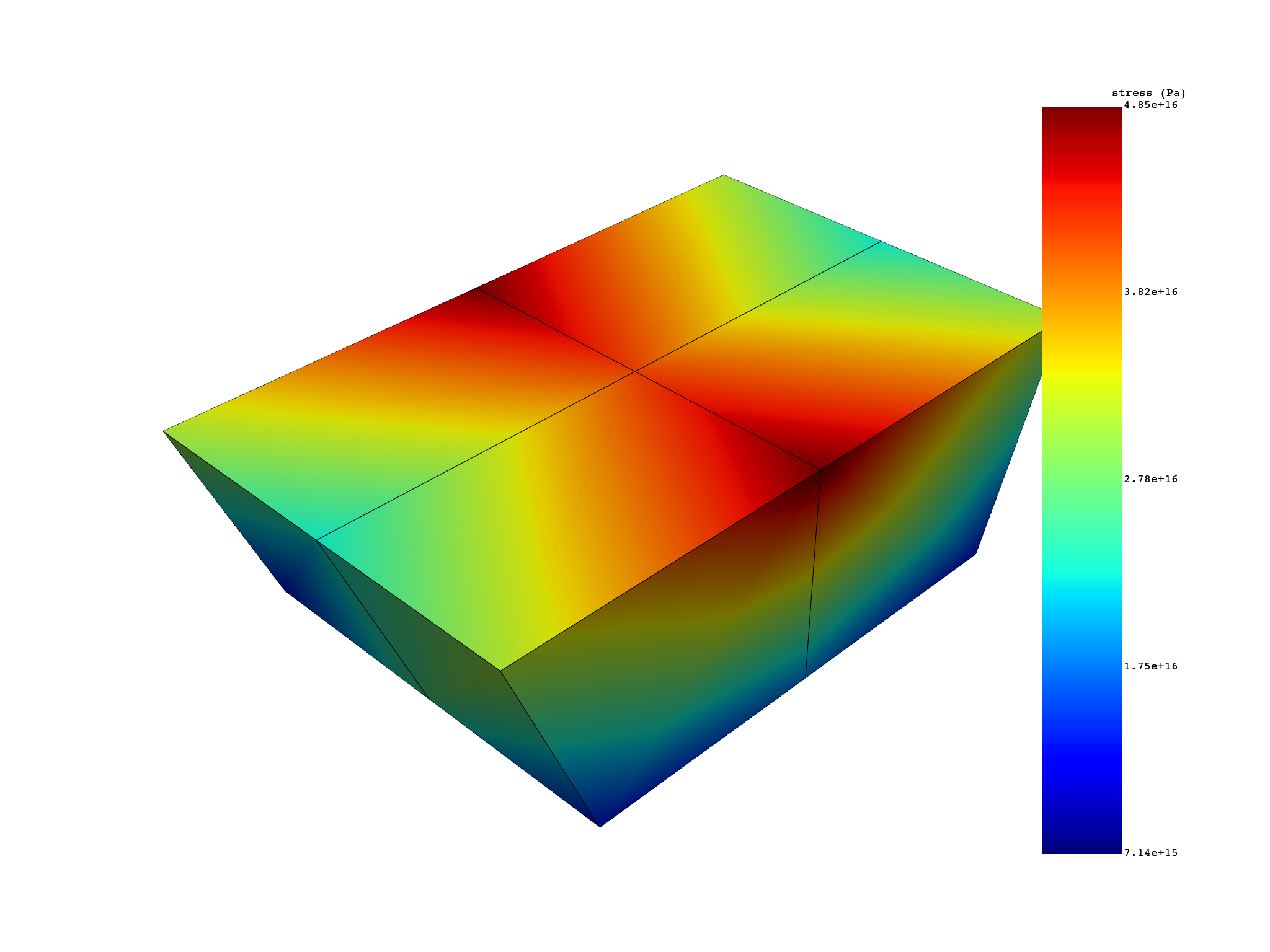
     results  S_VM (Pa)
     set_ids          1
 base_sector          1
    node_ids
           1 2.1648e+16
          14 2.6092e+16
          15 1.3073e+16
          18 1.8137e+16
           2 4.1523e+16
           6 2.2446e+16
         ...        ...


(None, <pyvista.plotting.plotter.Plotter object at 0x7fa4ae596500>)