Note
Go to the end to download the full example code.
Extract stress and strain invariants (static simulation)#
This example uses a static simulation to show how to extract a tensor’s stress and strain invariants.
Note
This example requires DPF 3.0 (2022 R1) or above. For more information, see PyDPF library compatibilities.
Perform required imports#
Perform required imports. This example uses a supplied file that you can
get by importing the DPF examples package.
from ansys.dpf import post
from ansys.dpf.post import examples
Get Simulation object#
Get the Simulation object that allows access to the result. The Simulation
object must be instantiated with the path for the result file. For example,
"C:/Users/user/my_result.rst" on Windows or "/home/user/my_result.rst"
on Linux.
example_path = examples.download_crankshaft()
# to automatically detect the simulation type, use:
simulation = post.load_simulation(example_path)
# to enable auto-completion, use the equivalent:
simulation = post.StaticMechanicalSimulation(example_path)
# print the simulation to get an overview of what's available
print(simulation)
Static Mechanical Simulation.
Data Sources
------------------------------
/opt/hostedtoolcache/Python/3.10.19/x64/lib/python3.10/site-packages/ansys/dpf/core/examples/result_files/crankshaft/crankshaft.rst
DPF Model
------------------------------
Static analysis
Unit system: MKS: m, kg, N, s, V, A, degC
Physics Type: Mechanical
Available results:
- node_orientations: Nodal Node Euler Angles
- displacement: Nodal Displacement
- velocity: Nodal Velocity
- acceleration: Nodal Acceleration
- reaction_force: Nodal Force
- stress: ElementalNodal Stress
- elemental_volume: Elemental Volume
- stiffness_matrix_energy: Elemental Energy-stiffness matrix
- artificial_hourglass_energy: Elemental Hourglass Energy
- kinetic_energy: Elemental Kinetic Energy
- co_energy: Elemental co-energy
- incremental_energy: Elemental incremental energy
- thermal_dissipation_energy: Elemental thermal dissipation energy
- elastic_strain: ElementalNodal Strain
- elastic_strain_eqv: ElementalNodal Strain eqv
- element_orientations: ElementalNodal Element Euler Angles
- structural_temperature: ElementalNodal Structural temperature
------------------------------
DPF Meshed Region:
69762 nodes
39315 elements
Unit: m
With solid (3D) elements
------------------------------
DPF Time/Freq Support:
Number of sets: 3
Cumulative Time (s) LoadStep Substep
1 1.000000 1 1
2 2.000000 1 2
3 3.000000 1 3
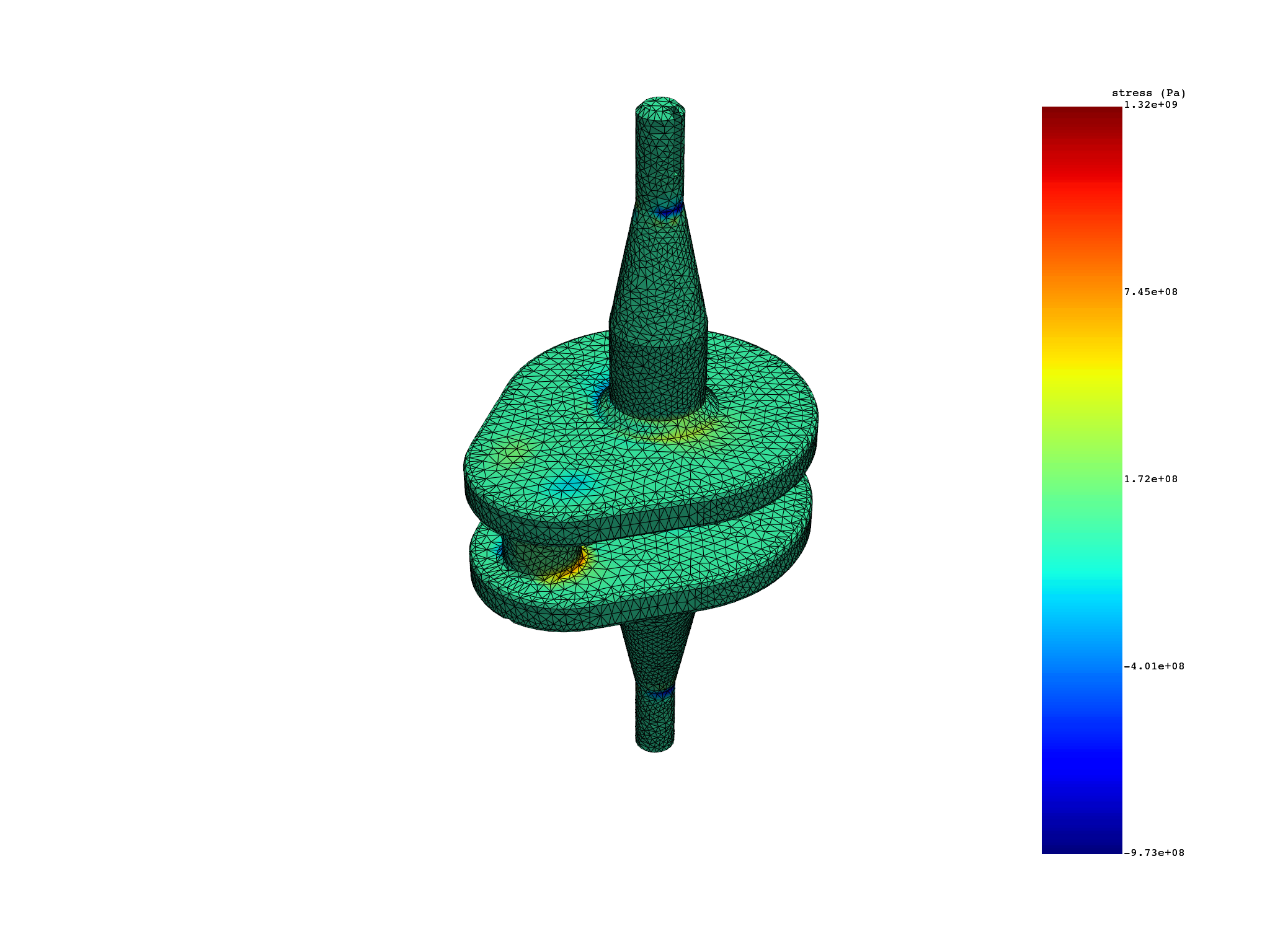
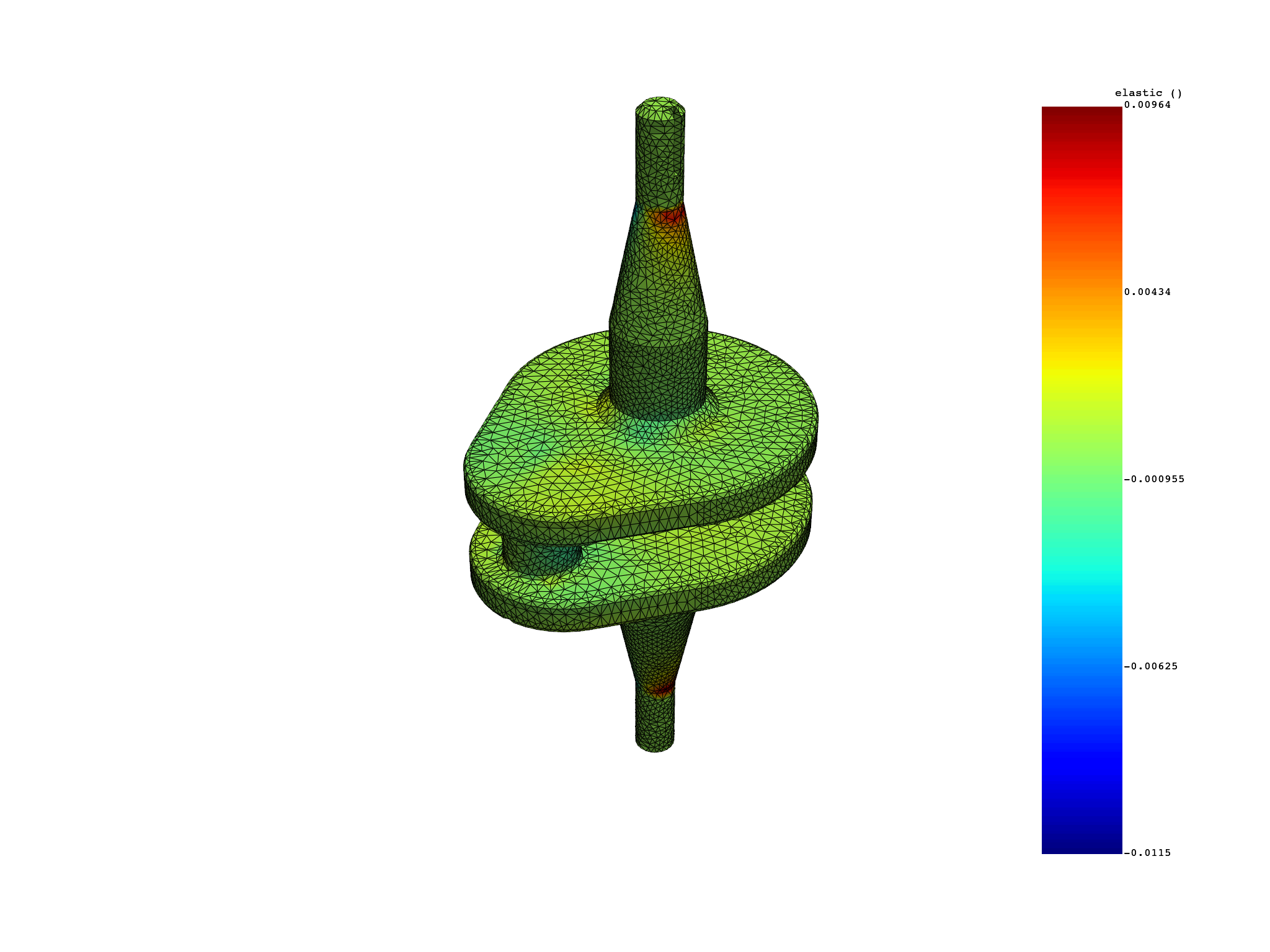
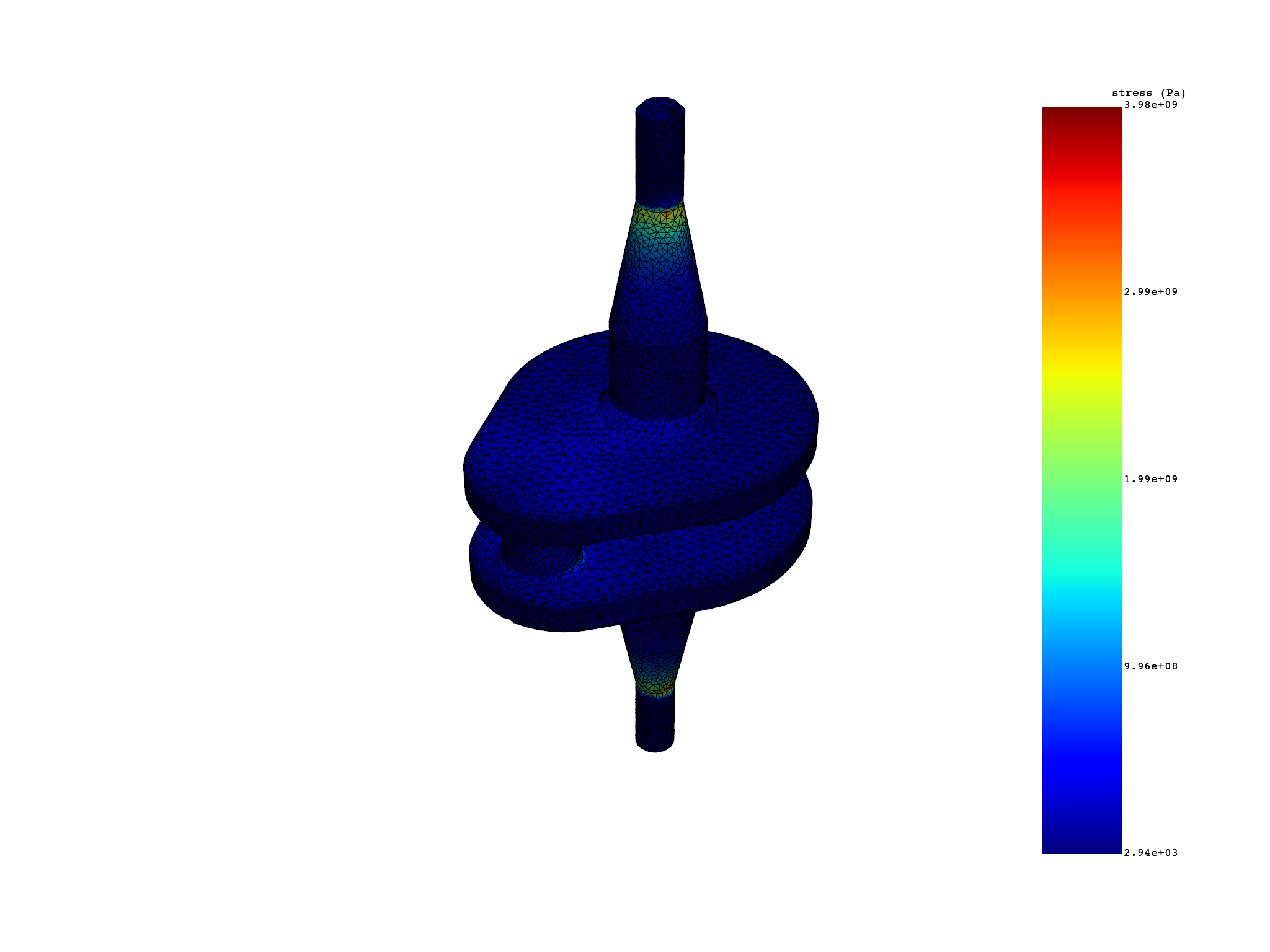
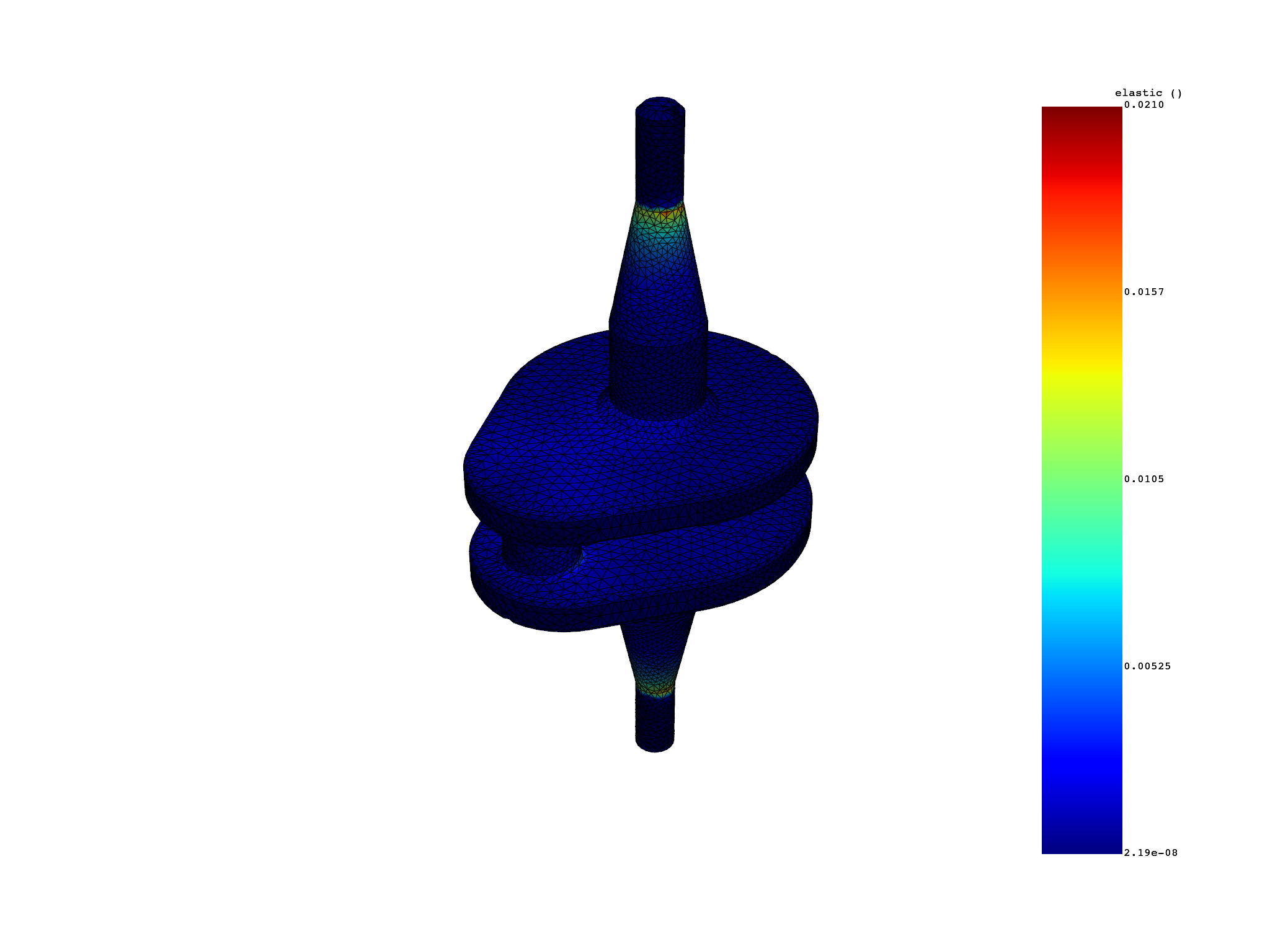
Extract elemental nodal stress and strain#
stress = simulation.stress(all_sets=True)
print(stress)
strain = simulation.elastic_strain(all_sets=True)
print(strain)
results S (Pa) ...
set_ids 1 2 ...
node 0 1 2 3 1 ...
element_ids components ...
18357 XX 2.7979e+06 4.7003e+05 -1.8736e+06 -3.3334e+06 4.3949e+06 -2.4906e+04 ...
YY 8.6092e+06 5.5603e+06 2.3814e+07 -2.2182e+07 2.8565e+07 2.1156e+07 ...
ZZ -1.0166e+07 1.1400e+06 3.2169e+07 -6.2071e+07 -2.6681e+06 1.4945e+07 ...
XY 5.9477e+05 1.0214e+07 5.3788e+07 5.2463e+07 7.8847e+05 1.9763e+07 ...
YZ -1.9866e+08 -1.6437e+08 -1.7338e+08 -1.5419e+08 -3.9727e+08 -3.2839e+08 ...
XZ -6.6205e+06 1.3030e+06 8.4608e+06 -9.4029e+06 -4.0082e+06 9.3691e+06 ...
... ... ... ... ... ... ... ... ...
results EPEL ...
set_ids 1 2 ...
node 0 1 2 3 1 ...
element_ids components ...
18357 XX 1.6326e-05 -7.7003e-06 -9.3343e-05 1.0971e-04 -1.6871e-05 -5.4276e-05 ...
YY 5.4098e-05 2.5387e-05 7.3628e-05 -1.2802e-05 1.4024e-04 8.3400e-05 ...
ZZ -6.7943e-05 -3.3456e-06 1.2793e-04 -2.7208e-04 -6.2781e-05 4.3027e-05 ...
XY 7.7320e-06 1.3278e-04 6.9924e-04 6.8201e-04 1.0250e-05 2.5692e-04 ...
YZ -2.5826e-03 -2.1368e-03 -2.2539e-03 -2.0045e-03 -5.1645e-03 -4.2691e-03 ...
XZ -8.6066e-05 1.6939e-05 1.0999e-04 -1.2224e-04 -5.2106e-05 1.2180e-04 ...
... ... ... ... ... ... ... ... ...