PyDPF-Post overview

This example provides an overview of how you use PyDPF-Post.

Perform required imports

Perform required imports. # This example uses a supplied file that you can get by importing the DPF examples package.

from ansys.dpf import post
from ansys.dpf.post import examples

Get Solution object

Get the Solution object that allows access to the result. The Solution object must be instantiated with the path for the result file. For example, "C:/Users/user/my_result.rst" on Windows or "/home/user/my_result.rst" on Linux.

solution = post.load_solution(examples.multishells_rst)

Get mesh and time frequency support

Get the mesh and time frequency support. The mesh is the support of the model. The time frequency support is the time/frequency representation of the model.

mesh = solution.mesh
time_freq_support = solution.time_freq_support

Get Result object

Get a Result object from the Solution object. The Result object can be a stress, plastic strain, elastic strain, temperature, or displacement.

post.print_available_keywords()
stress = solution.stress(location=post.locations.nodal, time_scoping=[1])

# Both location and ``time_scoping`` are available in the definition of
# the stress result.

stress.definition.location
stress.definition.time_scoping

print(stress)

element_scoping: list, int or dpf.core.Scoping
grouping: str. Use post.grouping.(...) as helper.
location: str. Use post.locations.(...) as helper.
mapdl_grouping: int. Write 186 to get mapdl_elements solid_186.
named_selection: str. Name of named_selection.
node_scoping: list, int or dpf.core.Scoping
path: DpfPath object that
            contains a list of coordinates,
            e.g. [[0.1, 0.0, 0.0],
            [0.0, 0.1, 0.0]].
set: int
time: float
time_scoping: list, int or dpf.core.Scoping

Stress Tensor object.

Object properties:
 - location   : Nodal
 - time_scoping : [1]

Compute data

Compute data.

SX subresult

This code gets the subresult SX, which is the stress tensor in the XX direction.

sx = stress.xx
sx.num_fields
sx_field = sx[0]
sx_data = sx.get_data_at_field(0)
print("Length of the data:", len(sx_data))
print()
print("Maximum Stress Field:\n", sx.max)
print()
print("Maximum data at stress field:", sx.max_data)
print("Maximum SX at Field 0:", sx.get_max_data_at_field(0))

Length of the data: 6854

Maximum Stress Field:
 DPF stress_1.s0 Field
  Location: Nodal
  Unit: Pa
  2 entities
  Data: 1 components and 2 elementary data

  IDs                   data(Pa)
  ------------          ----------
  0                     6.676153e+11

  1                     1.536714e+13




Maximum data at stress field: [6.67615284e+11 1.53671424e+13]
Maximum SX at Field 0: 667615283882.6666

Stress tensor result

This code gets the minimum and maximum stresses at a field for all directions (XX, XY, XZ, XY, YZ, and XZ.

s = stress.tensor
s_field = s[0]
s_data = sx.get_data_at_field(0)
print("Length of the data:", len(s_data))
print()
print("Maximum stress field:\n", s.max)
print()
print("Maximum data at stress field:", s.max_data)
print("Maximum stress tensors at field 0:\n", s.get_max_data_at_field(0))

print("Minimum stress field:\n", s.min)
print()
print("Minimum data at stress field:", s.min_data)
print("Minimum stress tensors at field 0:\n", s.get_min_data_at_field(0))

Length of the data: 6854

Maximum stress field:
 DPF stress_1.s Field
  Location: Nodal
  Unit: Pa
  2 entities
  Data: 6 components and 2 elementary data

  IDs                   data(Pa)
  ------------          ----------
  0                     6.676153e+11   8.744609e+11   4.953944e+11   6.018891e+11   1.103258e+11   1.855802e+11

  1                     1.536714e+13   4.217815e+08   3.782022e+12   2.079505e+11   1.579960e+11   1.099721e+12




Maximum data at stress field: [[6.67615284e+11 8.74460905e+11 4.95394439e+11 6.01889079e+11
  1.10325826e+11 1.85580244e+11]
 [1.53671424e+13 4.21781549e+08 3.78202198e+12 2.07950475e+11
  1.57995981e+11 1.09972131e+12]]
Maximum stress tensors at field 0:
 [6.67615284e+11 8.74460905e+11 4.95394439e+11 6.01889079e+11
 1.10325826e+11 1.85580244e+11]
Minimum stress field:
 DPF stress_1.s Field
  Location: Nodal
  Unit: Pa
  2 entities
  Data: 6 components and 2 elementary data

  IDs                   data(Pa)
  ------------          ----------
  0                     -5.779078e+11  -7.356049e+11  -2.412009e+11  -2.981459e+11  -2.421431e+11  -3.091386e+11

  1                     -1.496015e+13  -2.636956e+08  -3.779456e+12  -3.354327e+11  -1.571902e+11  -9.661232e+11




Minimum data at stress field: [[-5.77907764e+11 -7.35604867e+11 -2.41200931e+11 -2.98145939e+11
  -2.42143056e+11 -3.09138563e+11]
 [-1.49601458e+13 -2.63695614e+08 -3.77945626e+12 -3.35432675e+11
  -1.57190152e+11 -9.66123233e+11]]
Minimum stress tensors at field 0:
 [-5.77907764e+11 -7.35604867e+11 -2.41200931e+11 -2.98145939e+11
 -2.42143056e+11 -3.09138563e+11]

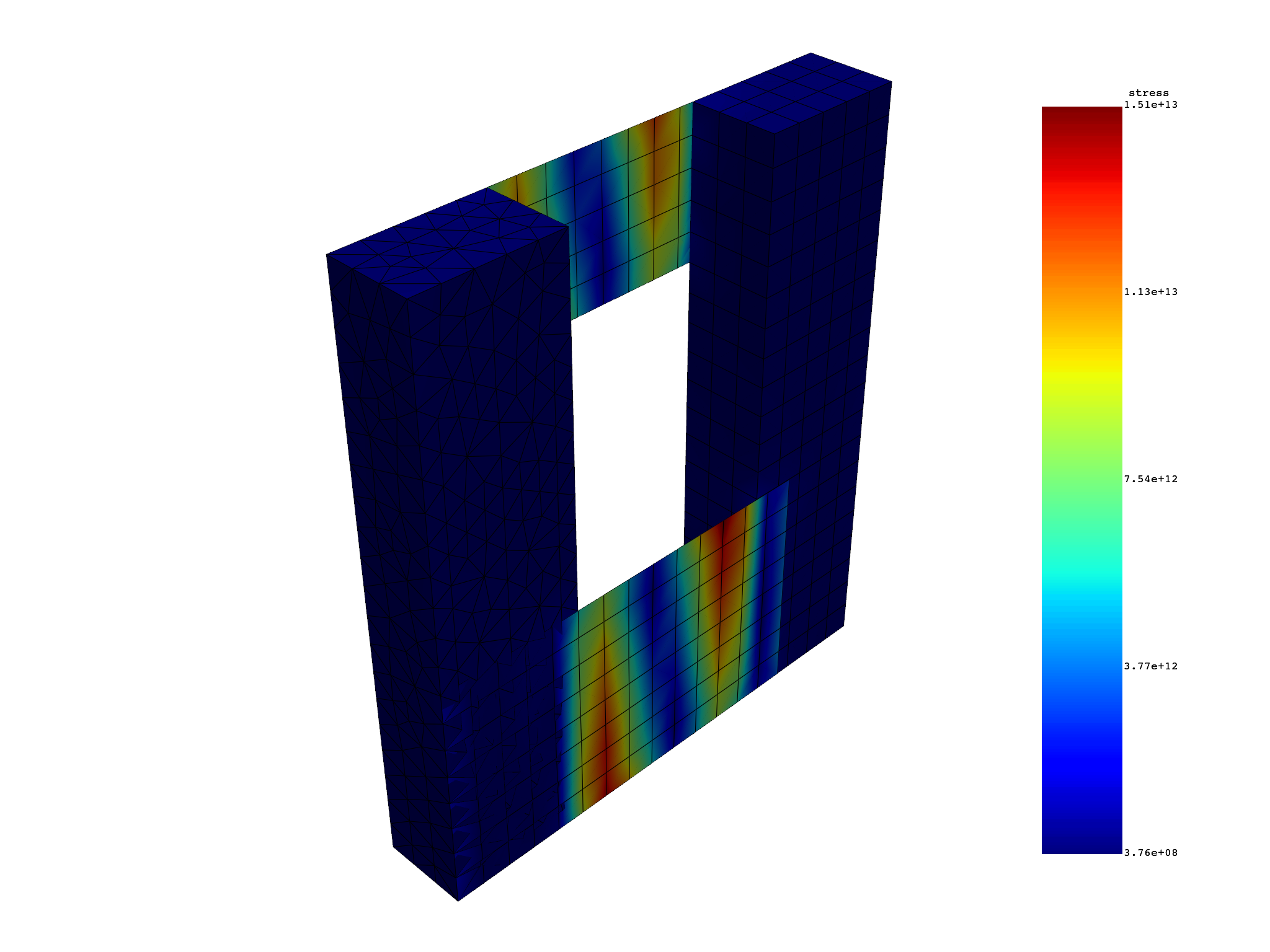
Plot result

Plot a result by using the plot_contour() method.

s.plot_contour()